What are hashes and hash functions?

Hashes and hash functions perform a vital role in both DLTs and wider computing security. A hash is often represented by a long alphanumeric value. It is generated through the act of ‘hashing’, by which an input (e.g. some text) is turned into an output. No matter the size of the input, the output will always be a fixed length as stipulated by the hash function. There are many different mathematical algorithms, known as hash functions, used to achieve this and they can be used for a variety of purposes.

How are hash functions used?‍

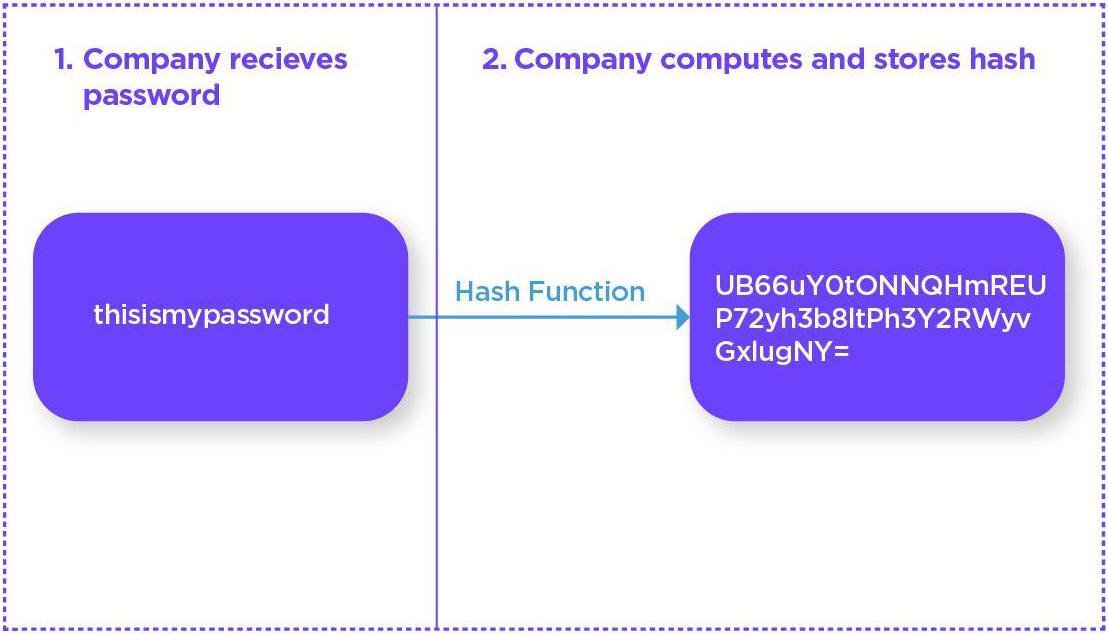
Hash functions are utilized by billions of users daily, as they form the basis of user security for website passwords. Owing to the risk of data breaches, companies do not (or should not) store your password as plain text. If they do and then suffer a hack then all of your other accounts with the same or similar passwords would also be compromised.

Companies therefore use your password as the input for the hash function and instead store the hashed output. When you log in they need only run the same hash function to ensure the outputs match. Please note that the process to correctly hash passwords is somewhat more complicated than is shown here in order to prevent dictionary and other lookup attacks, but not overly so.

Hash functions are also widely used by crypto assets. For example, Bitcoin uses a hash function known as SHA-256 for both mining and creating addresses. When creating new blocks, a Bitcoin miner solves a complex mathematical puzzle in order to find a block which is then appended to all prior blocks. This puzzle Is known as the Proof of Work and involves arranging a series of required data before running it through the hash function.

One part of the required data is the hash of the previous block. In this manner all hashes link back to the Genesis block. If I change block 1000, then the hash of blocks 1001 onwards would be incorrect (because the input would have changed). As such, to change an older block a malicious actor would have to have enough power to also change the blocks after it as otherwise the hashes wouldn’t match.

Why are hash functions used in DLTs?‍

The reason we use hash functions to help secure the network is because they boast several features which allow them to solve the types of security challenges outlined below:‍

Fast

We can quickly compute and compare two hashes together to verify that an input is correct. However, although it is quick to verify, for a sufficiently large hash function it is computationally infeasible to solve if you do not have the input. We can generate a hash almost instantly but deriving the input from the hash is very hard and slow. This is what allows us to use hash functions as they are quick to use for honest users but infeasible for malicious actors to break or reverse.‍

Efficient indexing‍

The shortened nature of the hash means they are useful for indexing and searching — as an example, a hash calculated using the SHA-256 algorithm is 256 bits or 32 bytes in length. As noted previously, the length of any given hash is fixed no matter how big the size of the input. This means we are able to index and search for these hashes as opposed to a large input. This is part of the reason why Bitcoin uses SHA-256 to generate public addresses – they are shorter than a public key. This helps reduce storage requirements and increase speed.‍

Input X will always give Output Y‍

The whole point of a hash function is that the hash of any given input will equal a fixed output. This cannot change because otherwise hashes could not be used for verification - we would be unable to compare to the input with any confidence.‍

Pre-image resistance‍

Pre-image resistance means that you cannot use the known output to determine the associated input. If we could work out an input through an output then we would be able to easily break the hash function, rendering the security useless. Instead of needing to expend large amounts of time and resources to solve a block for Bitcoin for example, it would be trivial for anyone to do so (and therefore also alter all old blocks). Hash functions protect against this, by making it hard (not impossible) to work out an input when you know the output.

The reason it is not impossible is because a malicious actor could brute force the function to discover the output of every input. However, this is extraordinarily difficult and realistically this computation (or series of computations) is impractical for any existing hardware). Although a malicious actor could get lucky and generate the output they were seeking earlier, the likelihood is that it would take them many, many lifetimes.‍

Avalanche Effect‍

Extending this slightly, hash functions also protect against deducing inputs based on marginal changes. Changing an input by one character does not change the output in a discoverable way and rather the whole output changes. This is known as the Avalanche Effect. For example, the SHA-256 hash of ‘Radix’ and ‘radix’ look very different:

Radix: 1f56d0be7dd66870efd22fb5073f8c1ae650dc6bad6e764d65327ad32c937c4f

radix: da7f85eaf3d0452479031da124d28778aaf15cc756a6c909d7dc708fade343f0‍

Collision resistance‍

Collision resistance means two different inputs are extremely unlikely to give the same output (known as a cryptographic hash collision). If two inputs regularly gave the same output then we would not be able to trust the veracity of network information. Again, we cannot fully eradicate the chance of these collisions but instead seek to make it exceedingly rare and as difficult as possible for malicious actors to take advantage of. It is worth noting, however, that certain hash functions like MD5 (not used in Radix) have been proven to suffer from a susceptibility to such collision attacks.‍

Second pre-image resistance‍

As noted, there is a chance that two inputs can give the same output, even if that is rare. Second pre-image resistance means that even in this event we should not be able to discover the second shared input.‍

How does Radix use hash functions?‍

The Radix ledger uses hash functions in four primary areas:

• Calculating digital signatures
• Public Key encryption / decryption
• Merkle Tree calculations
• Proof-of-Work (PoW) calculations

Calculating Digital Signatures

Calculating a digital signature using a public-key encryption algorithm for an arbitrary amount of data is usually too computationally expensive for high-volume use. In order to reduce the computational complexity, a hash of the input data is calculated, which provides a relatively small and fixed-length output. The signature is then calculated based on the hash of the underlying data and the sender's private key.

To verify the signature, a receiver of the data would calculate the hash themselves from the data, and validate that the signature matched this hash using the sender’s public key.This leverages several features of hashes:

• They are relatively cheap to compute (point 1)
• They always produce the same output for a given input (point 3); and
• Are highly resistant to collisions (point 6)

Public Key encryption / decryption

Because of the above-mentioned computational complexity of public-key encryption, most often a symmetric-key algorithm is used to encrypt the bulk of the data. Public-key methods are then used to encrypt the smaller symmetric-key, which is sent with the encrypted data.

The computational method to compute a symmetric-key for this kind of use is commonly called a Key Derivation Function (KDF). The collision resistance properties of hash functions make them useful as part of a KDF.‍

Merkle Tree calculations‍

To summarize, the relatively quick computation, compact size and collision resistance of hash functions make Merkle Trees (also known as Hash Trees) an important data structure for use in trustless systems.‍

Proof-of-Work‍

Many Proof-of-Work algorithms rely on the computational difficulty of producing a hash with specific values in specific locations within the hash. This difficulty is based on several properties of hashes, including pre-image resistance and the avalanche effect.

This post is designed to act as an overview to hashes and hash functions, as well as briefly explore how Radix utilizes them. In future posts we will cover a number of these topics in further detail, including digital signatures, public and symmetric key algorithms, generation and use of session keys, Merkle trees and Proof-of-Work algorithm.